[백준/JAVA] 17396번: 백도어
📖 문제
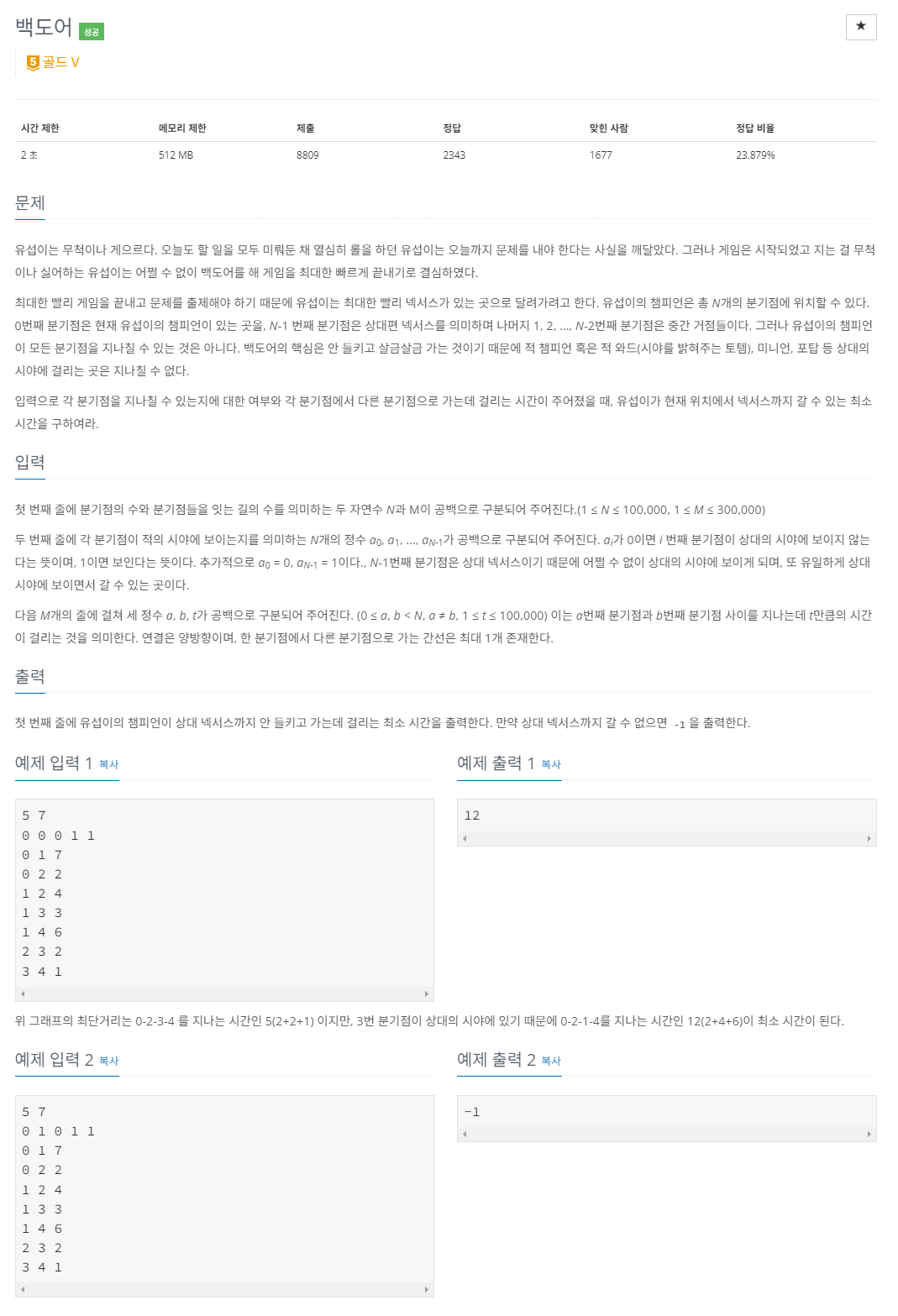
https://www.acmicpc.net/problem/17396
💡 풀이 방식
• 다익스트라
필요 자료구조
- 시야에 보이는지 여부 나타내는 1차원 boolean형 배열
- 그래프 인접 리스트
- 1 ~ N-1번 분기점이 까지 0번째 분기점까지 가는 데 걸리는 최소 시간 배열 (long형)
- 분기점 별 방문 표시를 나타내는 1차원 boolean형 배열
1. 각 분기점이 적의 시야에 보이는지 나타낸다.
sight = new boolean[N];
st = new StringTokenizer(br.readLine(), " ");
for(int i = 0 ; i < N ; i++) {
int num = Integer.parseInt(st.nextToken());
sight[i] = (num == 1) ? false : true;
}
2. 1 ~ N-1번 분기점이 까지 0번째 분기점까지 가는 데 걸리는 최소 시간 배열을 모두 최댓값인 Long.MAX_VALUE로 초기화한다.
dist = new long[N];
Arrays.fill(dist, Long.MAX_VALUE);
3. 그래프 정보를 양방향으로 입력받는다.
for(int i = 0 ; i < M ; i++) {
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int t = Integer.parseInt(st.nextToken());
graph[a].add(new Node(b, t));
graph[b].add(new Node(a, t));
}
4. 0번 점부터 다익스트라를 실행한다.
→ 우선순위 큐에 0번 점부터 넣는다.
그리고 0번 분기점과 연결된 분기점들 中
방문한 적 없고, 상대편 넥서스 (N-1번째 분기점) 가 아니고, 시야에 걸리지 않는 경우,
(현재 분기점에서의 최소 시간 + 다음 정점까지 걸리는 시간)의 값이 다음 정점까지의 최소 시간보다 작다면 이 값을 더 작은 값으로 갱신하고, 방문할 다음 정점과 최소 시간을 우선순위 큐에 추가한다.
private static void dijkstra() {
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(0,0));
dist[0] = 0;
while(!pq.isEmpty()) {
Node now = pq.poll();
if(visited[now.e]) continue;
visited[now.e] = true;
for(Node next : graph[now.e]) {
// 상대편 넥서스(N-1번째 분기점)거나 시야에 걸리는 경우 pass
if(next.e != N-1 && !sight[next.e]) continue;
if(dist[next.e] > dist[now.e] + next.v) {
dist[next.e] = dist[now.e] + next.v;
pq.add(new Node(next.e, dist[next.e]));
}
}
}
}
💥 유의사항
N이 최대 10만, t가 최대 10만이므로 10만*10만하면 int형 범위를 넘는다.
따라서 long형을 사용해야 한다.
🔺 코드
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
|
import java.util.*;
import java.io.*;
public class Main {
static final long INF = Long.MAX_VALUE;
static int N,M;
static boolean[] sight; // 시야에 보이는지 여부 나타나는 배열
static List<Node>[] graph;
static long[] dist; // 최소 시간 배열
static boolean[] visited;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine()," ");
N = Integer.parseInt(st.nextToken());
M = Integer.parseInt(st.nextToken());
// 각 분기점이 적의 시야에 보이는지 나타내는 배열
sight = new boolean[N];
st = new StringTokenizer(br.readLine(), " ");
for(int i = 0 ; i < N ; i++) {
int num = Integer.parseInt(st.nextToken());
sight[i] = (num == 1) ? false : true;
}
// 인접 그래프 초기화
graph = new ArrayList[N];
for(int i = 0 ; i < N ; i++) graph[i] = new ArrayList<>();
dist = new long[N];
Arrays.fill(dist, INF);
for(int i = 0 ; i < M ; i++) {
st = new StringTokenizer(br.readLine(), " ");
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
int t = Integer.parseInt(st.nextToken());
graph[a].add(new Node(b, t));
graph[b].add(new Node(a, t));
}
visited = new boolean[N];
dijkstra();
System.out.println(dist[N-1] == INF ? -1 : dist[N-1]);
}
private static void dijkstra() {
PriorityQueue<Node> pq = new PriorityQueue<>();
pq.add(new Node(0,0));
dist[0] = 0;
while(!pq.isEmpty()) {
Node now = pq.poll();
if(visited[now.e]) continue;
visited[now.e] = true;
for(Node next : graph[now.e]) {
// 상대편 넥서스(N-1번째 분기점)거나 시야에 걸리는 경우 pass
if(next.e != N-1 && !sight[next.e]) continue;
if(dist[next.e] > dist[now.e] + next.v) {
dist[next.e] = dist[now.e] + next.v;
pq.add(new Node(next.e, dist[next.e]));
}
}
}
}
}
class Node implements Comparable<Node> {
int e;
long v;
public Node(int e, long v) {
this.e = e;
this.v = v;
}
@Override
public int compareTo(Node n) {
return Long.compare(this.v, n.v);
}
}
|
cs |

💦 어려웠던 점
- 다익스트라인 점은 알았는데, 거리 갱신을 어떻게 할지?의 문제..
- 상대편 분기점(N-1번째 분기점)이거나 시야에 걸리는 경우 처리를 못 해줬다,,
- long형 처리,,
🧐 새로 알게 된 내용
- long형인 두 값을 오름차순 정렬하는 방법 : Long.compare(long v1, long v2)
@Override
public int compareTo(Node n) {
return Long.compare(this.v, n.v);
}
| 1회독 | 2회독 | 3회독 | 4회독 | 5회독 |
| V |
(참고)
✔ 풀이 참고
[백준] G5 17396 백도어 (java)
https://www.acmicpc.net/problem/17396 17396번: 백도어 첫 번째 줄에 분기점의 수와 분기점들을 잇는 길의 수를 의미하는 두 자연수 N과 M이 공백으로 구분되어 주어진다.(1 ≤ N ≤ 100,000, 1 ≤ M ≤ 300,000) 두
laugh4mile.tistory.com
[Java] 백준 17396 : 백도어
[문제] https://www.acmicpc.net/problem/17396 17396번: 백도어 첫 번째 줄에 분기점의 수와 분기점들을 잇는 길의 수를 의미하는 두 자연수 N과 M이 공백으로 구분되어 주어진다.(1 ≤ N ≤ 100,000, 1 ≤ M ≤ 300,
geumba.tistory.com