🔺 문제
코드트리 | 코딩테스트 준비를 위한 알고리즘 정석
국가대표가 만든 코딩 공부의 가이드북 코딩 왕초보부터 꿈의 직장 코테 합격까지, 국가대표가 엄선한 커리큘럼으로 준비해보세요.
www.codetree.ai
🔺 해결 아이디어
1) 최장 공통 부분 수열 LCS (DP)
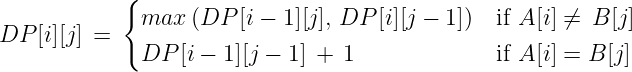
• 최소 편집 거리로 두 문자열 같게 만들기
= A에서 삭제를 진행해 A와 B의 LCS를 만들고, 삽입을 진행해 B를 만드는 것
- dp[i][j] : 문자열 A의 i번째까지와 문자열 B의 j번째까지를 활용해 만들 수 있는 LCS 길이
• 삭제 횟수 = A 길이 - LCS 길이
• 삽입 횟수 = B 길이 - LCS 길이
➡ 정답 = 삭제 횟수 + 삽입 횟수
2) 최소 편집 거리 String Matching (DP) 활용 ✅

- dp[i][j] : 문자열 A의 i번째까지, 문자열 B의 j번째까지의 둘 사이 편집거리
🔺 코드
1) 최장 공통 부분 수열 LCS (DP) 활용
- dp[i][j] : 문자열 A의 i번째까지와 문자열 B의 j번째까지를 활용해 만들 수 있는 LCS 길이
- LCS 길이 = 삭제 횟수 + 삽입 횟수
┕ 삭제 횟수 : A 길이 - LCS 길이 / 삽입 횟수 : B 길이 - LCS 길이
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
String A = "ABBBDAAA";
String B = "BADABBDBA";
int[][] dp = new int[A.length() + 1][B.length() + 1];
for(int i = 1 ; i <= A.length() ; i++) {
for(int j = 1 ; j <= B.length() ; j++) {
if(A.charAt(i - 1) == B.charAt(j - 1)) // 둘이 같은 경우
dp[i][j] = dp[i-1][j-1] + 1;
else // 둘이 다른 경우, 삽입 /삭제
dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);
}
}
// 삭제 횟수 = A 길이 - LCS
int delCnt = A.length() - dp[A.length()][B.length()];
// 삽입 횟수 = B 길이 - LCS
int addCnt = B.length() - dp[A.length()][B.length()];
System.out.println(delCnt + addCnt);
}
}
|
cs |
2) 최소 편집 거리 String Matching (DP) 활용
- dp[i][j] : 문자열 A의 i번째까지, 문자열 B의 j번째까지의 둘 사이 편집거리
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
|
import java.util.*;
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
String A = "ABBBDAAA";
String B = "BADABBDBA";
int[][] dp = new int[A.length() + 1][B.length() + 1];
// dp 배열 초기화 (i번 삭제/삽입 그대로 발생)
for(int i = 1 ; i < dp.length ; i++) {
dp[i][0] = i;
}
for(int i = 1 ; i < dp[0].length ; i++) {
dp[0][i] = i;
}
for(int i = 1 ; i <= A.length() ; i++) {
for(int j = 1 ; j <= B.length() ; j++) {
// 문자열 A의 i번째 글자 == 문자열 B의 j번째 글자인 경우
if(A.charAt(i - 1) == B.charAt(j - 1))
dp[i][j] = dp[i-1][j-1];
// 다른 경우, 삽입 /삭제
else
dp[i][j] = Math.min(dp[i-1][j], dp[i][j-1]) + 1;
}
}
System.out.println(dp[A.length()][B.length()]); // 결과 : 7
}
}
|
cs |
dp 수행 결과는 다음과 같다.

💬 느낀 점
LCS는 몇 번 풀어봤는데
최소 편집 거리 문제는 처음 접해본다!
코드트리 진짜 체계적이고 좋은 거 같다
왜 진즉 안했을까...💦💦
복습 많이 해서 무럭무럭 자라야지,,,🙌🙌
| 1회독 | 2회독 | 3회독 | 4회독 | 5회독 |
| V |
(참고)
LCS (최장 공통 부분 수열)
📍 정의 및 특징 두 수열이 주어졌을 때, 모두의 부분 수열이 되는 수열 중 가장 긴 것을 찾는 문제 - DP의 일종 - 문제 유형 : 최장 공통 부분 수열 길이 구하기, 최장 공통 부분 수열 구하기 #DP
bono039.tistory.com
'코테 > 코드트리' 카테고리의 다른 글
| [코드트리/NOVICE HIGH] 네비게이션 (JAVA) (0) | 2023.09.22 |
|---|---|
| [코드트리/NOVICE HIGH] 쪼개어 배낭 채우기 2 (JAVA) (0) | 2023.09.20 |
| [코드트리/NOVICE HIGH] 숫자 암호 만들기 (JAVA) (0) | 2023.09.15 |
| [코드트리/NOVICE MID] 중앙값 계산 2 (JAVA) (0) | 2023.09.11 |
| [코드트리/NOVICE MID] 그 계절, 그 날 (JAVA) (0) | 2023.09.11 |
